Advertisements
Advertisements
Question
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
Solution
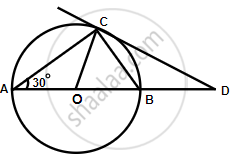
Join OC,
∠BCD = ∠BAC = 30° ...(Angles in alternate segment)
Arc BC subtends ∠DOC at the centre of the circle and ∠BAC at the remaining part of the circle.
∴ ∠BOC = 2∠BAC = 2 × 30° = 60°
Now in ΔOCD,
∠BOC or ∠DOC = 60°
∠OCD = 90° ...(OC ⊥ CD)
∴ ∠DCO + ∠ODC = 90°
`=>` 60° + ∠ODC = 90°
`=>` ∠ODC = 90° – 60° = 30°
Now in ΔBCD,
∵ ∠ODC or ∠BDC = ∠BCD = 30°
∴ BC = BD
APPEARS IN
RELATED QUESTIONS
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
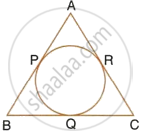
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
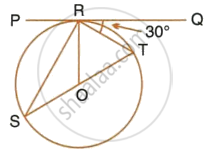
Given O is the centre of the circle and angle TRQ = 30°.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

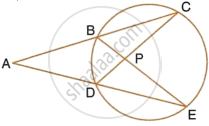
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
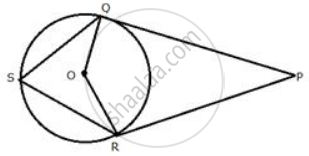
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
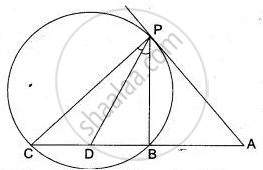
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
