Advertisements
Advertisements
Question
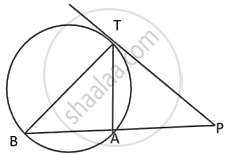
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
Solution
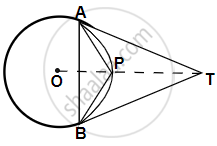
Join PB.
In ΔTAP and ΔTBP,
TA = TB ...(Tangents segments from an external points are equal in length)
Also, ∠ATP = ∠BTP. ...(Since OT is equally inclined with TA and TB)
TP = TP ...(Common)
`=>` ΔTAP ≅ ΔTBP ...(By SAS criterion of congruency)
`=>` ∠TAP = ∠TBP ...(Corresponding parts of congruent triangles are equal)
But ∠TBP = ∠BAP ...(Angles in alternate segments)
Therefore, ∠TAP = ∠BAP.
Hence, AP bisects ∠TAB.
APPEARS IN
RELATED QUESTIONS
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

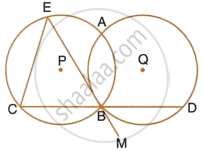
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
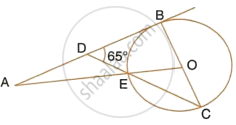
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
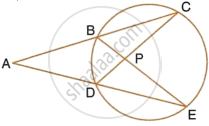
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
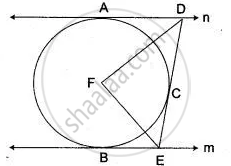
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

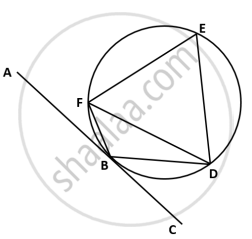
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ:
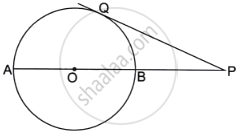
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.