Advertisements
Advertisements
Question
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
Solution
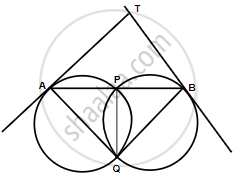
Join PQ.
AT is tangent and AP is a chord.
∴ ∠TAP = ∠AQP (Angles in alternate segments) ...(i)
Similarly, ∠TBP = ∠BQP ...(ii)
Adding (i) and (ii)
∠TAP + ∠TBP = ∠AQP + ∠BQP
`=>` ∠TAP + ∠TBP = ∠AQB ...(iii)
Now in ΔTAB,
∠ATB + ∠TAP + ∠TBP = 180°
`=>` ∠ATB + ∠AQB = 180°
Therefore, AQBT is a cyclic quadrilateral.
Hence, A, Q, B and T lie on a circle.
APPEARS IN
RELATED QUESTIONS
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
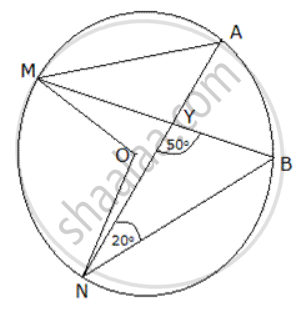
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
In following fig., O is the centre of the circle. Find ∠ CBD.
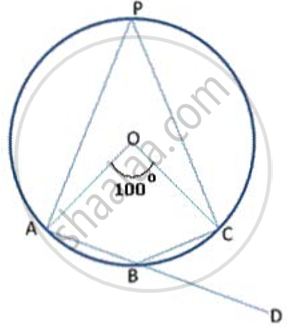
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
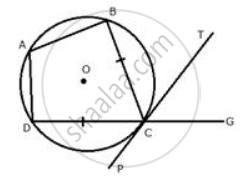
If O is the centre of the circle, find the value of x in each of the following figures
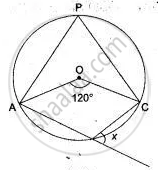
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.