Advertisements
Advertisements
प्रश्न
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
उत्तर
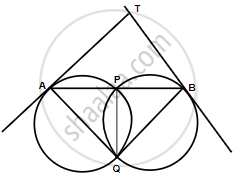
Join PQ.
AT is tangent and AP is a chord.
∴ ∠TAP = ∠AQP (Angles in alternate segments) ...(i)
Similarly, ∠TBP = ∠BQP ...(ii)
Adding (i) and (ii)
∠TAP + ∠TBP = ∠AQP + ∠BQP
`=>` ∠TAP + ∠TBP = ∠AQB ...(iii)
Now in ΔTAB,
∠ATB + ∠TAP + ∠TBP = 180°
`=>` ∠ATB + ∠AQB = 180°
Therefore, AQBT is a cyclic quadrilateral.
Hence, A, Q, B and T lie on a circle.
APPEARS IN
संबंधित प्रश्न
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
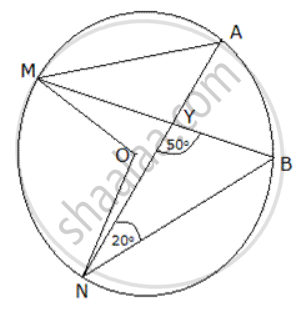
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
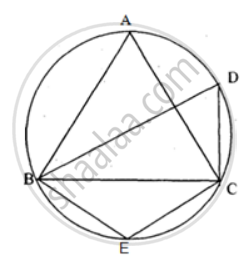
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

