Advertisements
Advertisements
प्रश्न
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

उत्तर

i. ∠DBC = ∠DAC = 27°
(Angle subtended by the same chord on the circle are equal)
ii. ∠ACB = ∠ADB = 33°
∠ACD = ∠ABD = 50°
(Angle subtended by the same chord on the circle are equal)
∴ ∠DCB = ∠ACD + ∠ACB
= 50° + 33°
= 83°
iii. ∠DAB + ∠DCB = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` 27° + ∠CAB + ∠83° = 180°
`=>` ∠CAB = 180° – 110° = 70°
APPEARS IN
संबंधित प्रश्न
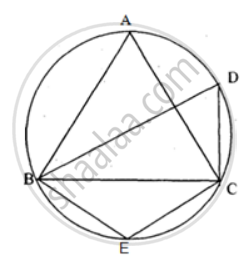
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
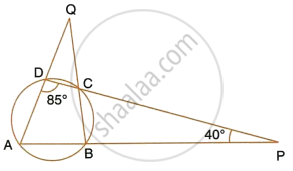
Use the given figure to find:
- ∠BAD,
- ∠DQB.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the figure, given below, find: ∠ABC. Show steps of your working.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
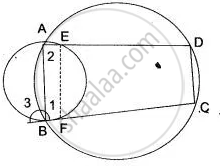
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
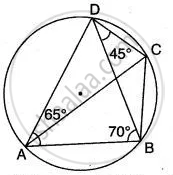
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.