Advertisements
Advertisements
प्रश्न
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
उत्तर
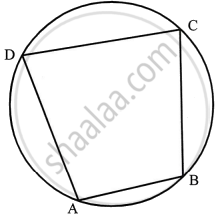
ABCD is a cyclic quadrilateral.
∴ ∠A + ∠C = 180°
`=>` 3∠C + ∠C = 180°
`=>` 4∠C = 180°
`=>` ∠C = 45°
∵ ∠A = 3∠C
`=>` ∠A = 3 × 45°
`=>` ∠A = 135°
Similarly,
∴ ∠B + ∠D = 180°
`=>` ∠B + 5∠B = 180°
`=>` 6∠B = 180°
`=>` ∠B = 30°
∵ ∠D = 5∠B
`=>` ∠D = 5 × 30°
`=>` ∠D = 150°
Hence, ∠A = 135°, ∠B = 30°, ∠C = 45°, ∠D = 150°
APPEARS IN
संबंधित प्रश्न
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
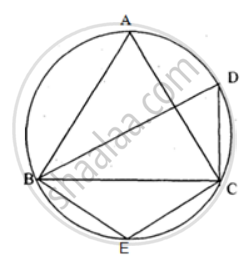
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
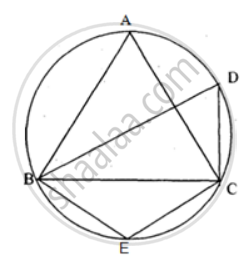
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
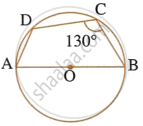
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
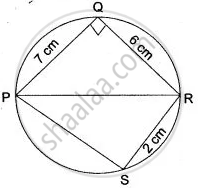
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.