Advertisements
Advertisements
प्रश्न
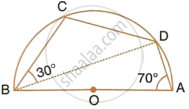
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
उत्तर
Since ABCD is a cyclic quadrilateral, therefore, ∠BCD + ∠BAD = 180° ...(Since opposite angles of a cyclic quadrilateral are supplementary)
`=>` ∠BCD + 70° = 180°
`=>` ∠BCD = 180° − 70° = 110°
In ΔBCD, we have,
∠CBD + ∠BCD + ∠BDC = 180°
`=>` 30° + 110° + ∠BDC = 180°
`=>` ∠BDC = 180° − 140°
`=>` ∠BDC = 40°
APPEARS IN
संबंधित प्रश्न
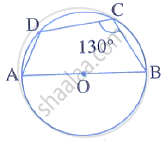
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
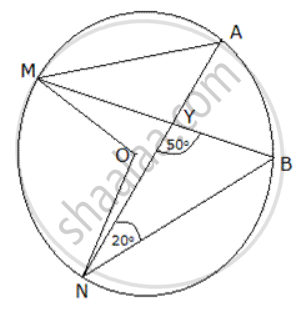
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
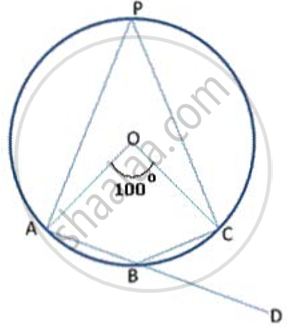
In following fig., O is the centre of the circle. Find ∠ CBD.
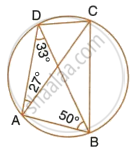
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
