Advertisements
Advertisements
प्रश्न
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
उत्तर
Consider the arc BCD of the circle. This arc makes an angle ∠BOD = 160° at the centre of the circle and ∠BAD at a point A on the circumference.

∴ ∠BAD = `1/2`∠BOD = 80°
Now, ABPD is a cyclic quadrilateral.
∴ ∠BAD + ∠BPD = 180°
⇒ 80° + ∠BPD = 180°
⇒ ∠BPD = 180° - 80°
⇒ ∠BPD = 100°
⇒ ∠BCD = 100° ....(∵∠BPD and ∠BCD are angles in the same segment. ∴∠BCD = ∠BPD = 100°)
APPEARS IN
संबंधित प्रश्न
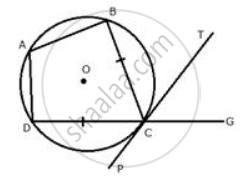
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
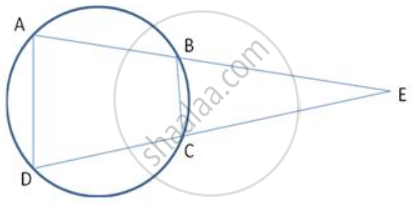
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In the following figure, Prove that AD is parallel to FE.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
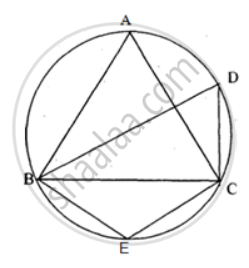
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
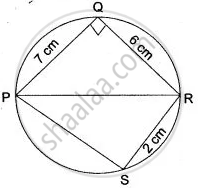
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.