Advertisements
Advertisements
प्रश्न
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

उत्तर
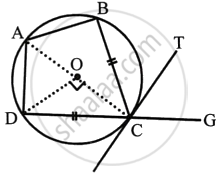
Join OC, OD and AC
i. ∠BCG + ∠BCD = 180° ...(Linear pair)
`=>` 108° + ∠BCD = 180° ...(∵ ∠BCG = 108° given)
`=>` ∠BCD = 180° – 108° = 72°
BC = CD ...(Given)
∴ ∠DCP = ∠BCT
But, ∠BCT + ∠BCD + ∠DCP = 180°
∴ ∠BCT + ∠BCT + 72° = 180° ...(∵ ∠DCP = ∠BCT)
2∠BCT = 180° – 72° = 108°
∴ ∠BCT = `108^circ/2` = 54°
ii. PCT is a tangent and CA is a chord.
∠CAD = ∠BCT = 54°
But arc DC subtends ∠DOC at the centre and ∠CAD at the remaining part of the circle.
∴ ∠DOC = 2∠CAD
= 2 × 54°
= 108°
APPEARS IN
संबंधित प्रश्न
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
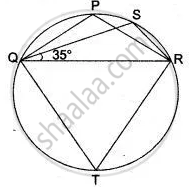
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the figure, given below, find: ∠ABC. Show steps of your working.

The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.