Advertisements
Advertisements
प्रश्न
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
उत्तर
Let ABCD be a cyclic quadrilateral such that its diagonals AC and BD intersect in P at right angles.
Let PL ⊥ AB such that LP produced to meet CD in M. We have to prove that M bisects CD. i.e.,
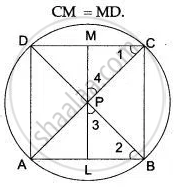
Consider arc AD, Clearly, it makes angles ∠ 1 and ∠2 in the same segment.
∠ 1 = ∠ 2 ...(i)
In the right-angled triangle PLB, we have
∠ 2 + ∠ 3 + ∠ PLB = 180°
⇒ ∠ 2 + ∠ 3 + 90° = 180°
⇒ ∠ 2 + ∠ 3 = 90° ....(ii)
Since, LPM is a straight line.
∴ ∠ 3 + ∠ BPD + ∠ 4 = 180°
⇒ ∠ 3 + 90° + ∠ 4 = 180°
⇒ ∠ 3 + ∠ 4 = 90° ...(iii)
From (ii) and (iii), we get
∠ 2 + ∠ 3 = ∠ 3 + ∠ 4
∠ 2 = ∠ 3 ...(iv)
From (i) and (iv), we get
∠ 1 = ∠ 4
PM = CM
Similarly,
PM = DM
Hence, CM = MD
Hence proved.
APPEARS IN
संबंधित प्रश्न
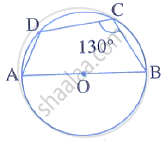
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
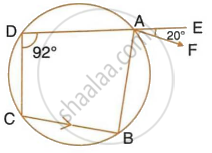
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
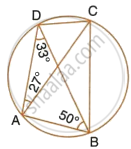
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

