Advertisements
Advertisements
प्रश्न
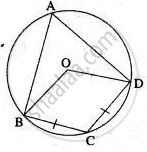
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

उत्तर
Given
`{:(∠ABC = 100^circ),(∠ACD = 40^circ):}}` ...(Given)
∠ABC + ∠ACD = 180° ...(Opposite angles of a cyclic quadrilateral)
100° + ∠ADC = 180°
∴ ∠ADC = 180° – 100° = 80°
Also,
∠ACD + ∠ADC + ∠CAD = 180° ...(Sum of angles of a triangle)
40° + 80° + ∠CAD = 180°
∠CAD = 180° – 120° = 60°
Now, ∠DCT = ∠CAD = 60° ...(Alternate segment theorem)
APPEARS IN
संबंधित प्रश्न
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
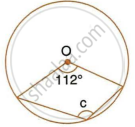
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the following figure, Prove that AD is parallel to FE.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
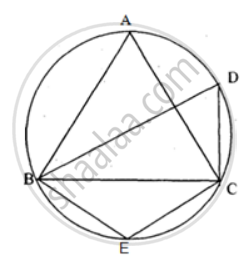
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
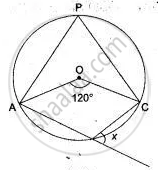
If O is the centre of the circle, find the value of x in each of the following figures
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.