Advertisements
Advertisements
Question
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

Solution
Given
`{:(∠ABC = 100^circ),(∠ACD = 40^circ):}}` ...(Given)
∠ABC + ∠ACD = 180° ...(Opposite angles of a cyclic quadrilateral)
100° + ∠ADC = 180°
∴ ∠ADC = 180° – 100° = 80°
Also,
∠ACD + ∠ADC + ∠CAD = 180° ...(Sum of angles of a triangle)
40° + 80° + ∠CAD = 180°
∠CAD = 180° – 120° = 60°
Now, ∠DCT = ∠CAD = 60° ...(Alternate segment theorem)
APPEARS IN
RELATED QUESTIONS
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
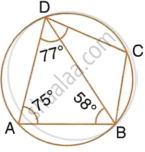
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
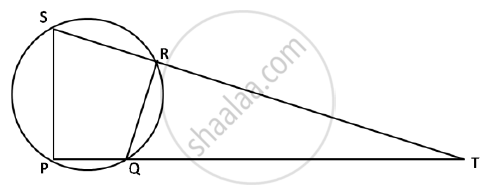
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
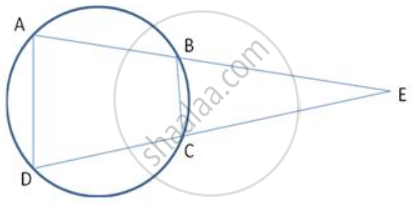
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
In the following figure, Prove that AD is parallel to FE.

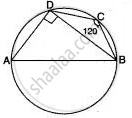
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA