Advertisements
Advertisements
Question
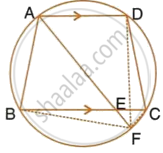
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Solution
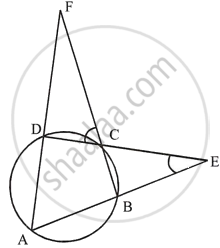
Given – In a circle, ABCD is a cyclic quadrilateral AB and DC are produced to meet at E and BC and AD are produced to meet at F.
∠DCF : ∠F : ∠E = 3 : 5 : 4
Let ∠DCF = 3x, ∠F = 5x, ∠E = 4x
Now, we have to find, ∠A, ∠B, ∠C and ∠D
In cyclic quad. ABCD, BC is produced.
∴ ∠A = ∠DCF = 3x
In ΔCDF,
Ext ∠CDA = ∠DCF + ∠F = 3x + 5x = 8x
In ΔBCE,
Ext ∠ABC = ∠BCE + ∠E ...[∠BCE = ∠DCF, Vertically opposite angles]
= ∠DCF + ∠E
= 3x + 4x
= 7x
Now, in cyclic quad ABCD,
Since, ∠B + ∠D = 180° ...[Since sum of opposite of a cyclic quadrilateral are supplementary]
`=>` 7x + 8x = 180°
`=>` 15x = 180°
`=> x = (180^circ)/15 = 12^circ`
∠A = 3x = 3 × 12° = 36°
∠B = 7x = 7 × 12° = 84°
∠C = 180° – ∠A = 180° – 36° = 144°
∠D = 8x = 8 × 12° = 96°
APPEARS IN
RELATED QUESTIONS
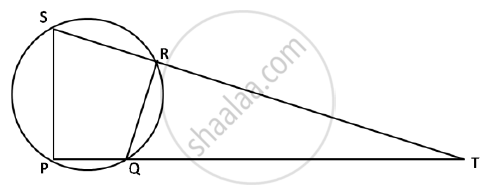
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
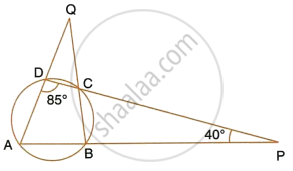
Use the given figure to find:
- ∠BAD,
- ∠DQB.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
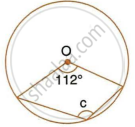
In the following figure, O is the centre of the circle. Find the values of a, b and c.
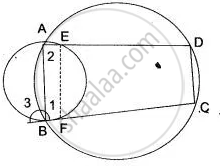
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
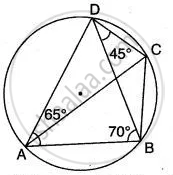
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.