Advertisements
Advertisements
Question
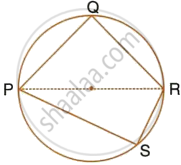
The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.
Solution
In the figure, PQRS is a cyclic quadrilateral in which PR is a diameter
PQ = 7 cm
QR = 3RS = 6 cm
3RS = 6 cm
RS = 2 cm
Now in ∆PQR,
∠Q = 90° ...[Angles in a semi-circle]
∴ PR2 = PQ2 + QR2 ...[Pythagoras theorem]
= 72 + 62
= 49 + 36
= 85
Again in right ΔPSQ,
PR2 = PS2 + RS2
`=>` 85 = PS2 + 22
`=>` PS2 = 85 – 4 = 81 = (9)2
∴ PS = 9 cm
Now, perimeter of quad PQRS
= PQ + QR + RS + SP
= (7 + 9 + 2 + 6) cm
= 24
APPEARS IN
RELATED QUESTIONS
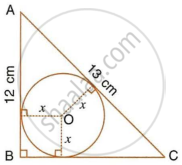
ABC is a right angles triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
Calculate the value of x, the radius of the inscribed circle.
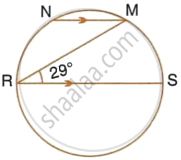
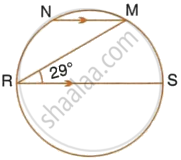
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBC
Also, show that the ΔAOD is an equilateral triangle.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠ADC
Also, show that the ΔAOD is an equilateral triangle.
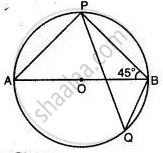
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
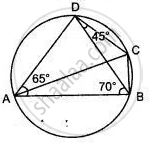
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
In the figure given alongside, AD is the diameter of the circle. If ∠ BCD = 130°, Calculate: (i) ∠ DAB (ii) ∠ ADB.
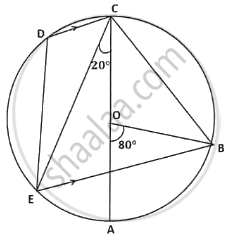
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED