Advertisements
Advertisements
Question
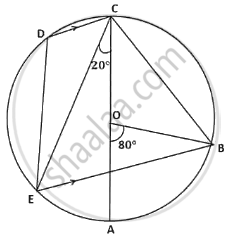
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED
Solution
a. ∠BOC = 180° – 80° = 100°
`\implies` ∠BEC = `1/2 xx 100^circ` = 50° ...(∠ at centre is twice the ∠ in remaining segment)
b. ∠BCD = ∠BCA + ∠ACE + ∠ECD
= 40° + 20° + 50°
= 110°
c. ∠CED = 180° – 110° – 50° = 20°
APPEARS IN
RELATED QUESTIONS
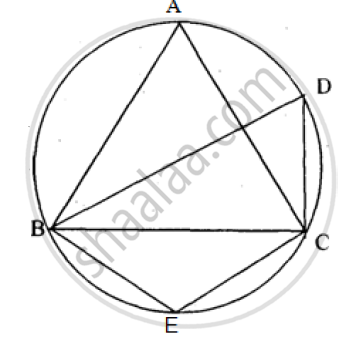
In the figure, m∠DBC = 58°. BD is the diameter of the circle. Calculate:
1) m∠BDC
2) m∠BEC
3) m∠BAC
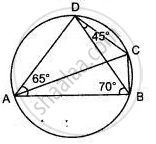
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Prove that the rhombus, inscribed in a circle, is a square.
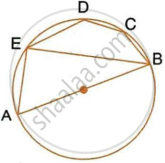
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate:
- ∠DAB,
- ∠DBA,
- ∠DBC,
- ∠ADC.
Also, show that the ΔAOD is an equilateral triangle.
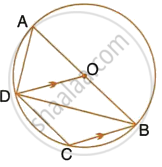
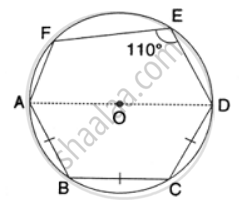
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
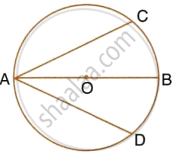
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
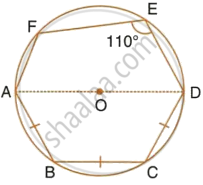
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.