Advertisements
Advertisements
प्रश्न
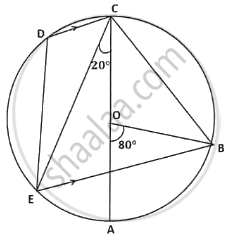
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED
उत्तर
a. ∠BOC = 180° – 80° = 100°
`\implies` ∠BEC = `1/2 xx 100^circ` = 50° ...(∠ at centre is twice the ∠ in remaining segment)
b. ∠BCD = ∠BCA + ∠ACE + ∠ECD
= 40° + 20° + 50°
= 110°
c. ∠CED = 180° – 110° – 50° = 20°
APPEARS IN
संबंधित प्रश्न
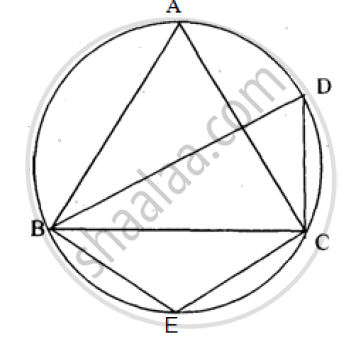
In the figure, m∠DBC = 58°. BD is the diameter of the circle. Calculate:
1) m∠BDC
2) m∠BEC
3) m∠BAC
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

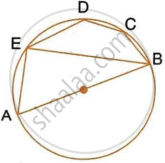
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
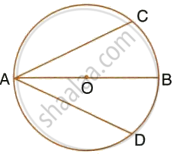
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
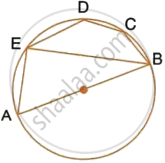
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBC
Also, show that the ΔAOD is an equilateral triangle.

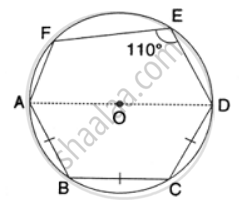
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
In the figure, ∠DBC = 58°. BD is diameter of the circle.
Calculate:
- ∠BDC
- ∠BEC
- ∠BAC