Advertisements
Advertisements
प्रश्न
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

उत्तर
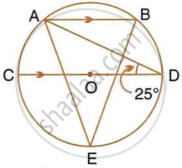
Join AC and BD
∴ ∠CAD = 90° and ∠CBD = 90°
(Angle in a semicircle is a right angle)
Also, AB || CD
∴ ∠BAD = ∠ADC = 25° ...(Alternate angles)
∠BAC = ∠BAD + ∠CAD
= 25° + 90°
= 115°
∴ ∠ADB = 180° – 25° – ∠BAC
= 180° – 25° – 115°
= 40°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
Also, ∠AEB = ∠ADB = 40°
(Angle subtended by the same chord on the circle are equal)
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

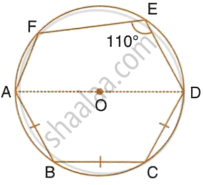
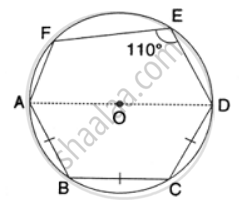
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBC
Also, show that the ΔAOD is an equilateral triangle.

In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
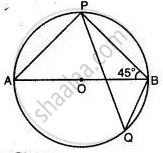
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
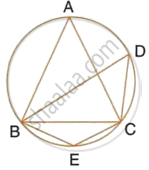
In the figure, ∠DBC = 58°. BD is diameter of the circle.
Calculate:
- ∠BDC
- ∠BEC
- ∠BAC
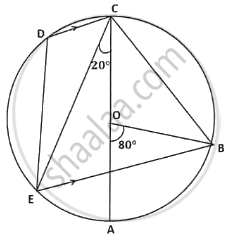
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED