Advertisements
Advertisements
प्रश्न
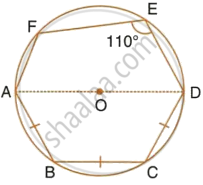
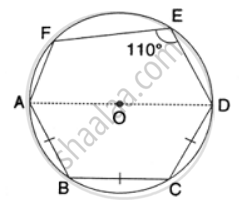
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
उत्तर
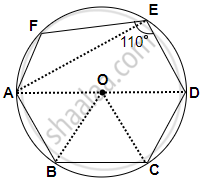
Join AE, OB and OC
∵ AOD is the diameter,
∴ ∠AED = 90° ...[Angle in a semi-circle]
But ∠DEF = 110° ...[Given]
∴ ∠AEF = ∠DEF – ∠AED
= 110° – 90°
= 20°
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Prove that the parallelogram, inscribed in a circle, is a rectangle.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
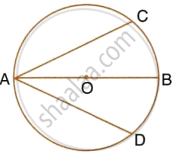
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
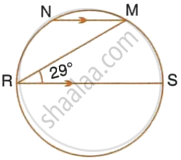
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.