Advertisements
Advertisements
प्रश्न
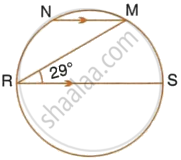
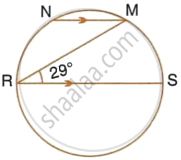
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
उत्तर
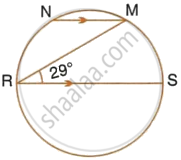
Also, RS || NM
∴ ∠NMR = ∠MRS = 29° ...(Alternate angles)
∴ ∠NMS = 90° + 29° = 119°
Also, ∠NRS + ∠MS = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` ∠NMR + 29° + 119° = 180°
`=>` ∠NRM = 180° – 148°
∴ ∠NRM = 32°
APPEARS IN
संबंधित प्रश्न
Calculate the area of the shaded region, if the diameter of the semicircle is equal to 14 cm. Take `pi = 22/7`

Prove that the rhombus, inscribed in a circle, is a square.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
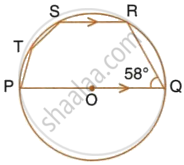
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°,
Calculate:
- ∠RPQ,
- ∠STP.
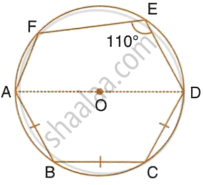
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
In the figure, given below, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, fins the distance MN between the two chords of lengths 24 cm and 18 cm respectively.

In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
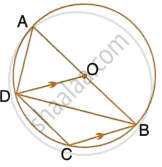
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
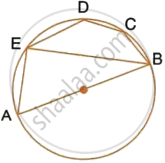
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.