Advertisements
Advertisements
प्रश्न
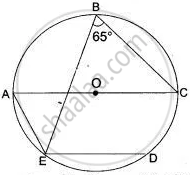
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.
उत्तर
Consider the arc CDE. We find that ∠ CBE and ∠ CAE are the angles in the same segment of arc CDE.
∴ ∠ CAE = ∠ CBE
⇒ ∠ CAE = 65° ...( ∵ ∠ CBE = 65° )
Since AC is the diameter of the circle and the angle in a semicircle is a right angle.
Therefore, ∠ AEC = 90°.
Now, in Δ ACE, we have
∠ ACE + ∠ AEC + ∠ CAE = 180°
⇒ ∠ ACE + 90° + 65° = 180°
⇒ ∠ ACE = 25°
But ∠ DEC and ∠ ACE are alternate angles, because AC || DE.
∴ ∠ DEC = ∠ ACE = 25°.
APPEARS IN
संबंधित प्रश्न
In the figure, m∠DBC = 58°. BD is the diameter of the circle. Calculate:
1) m∠BDC
2) m∠BEC
3) m∠BAC
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
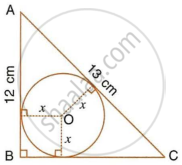
ABC is a right angles triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
Calculate the value of x, the radius of the inscribed circle.
Prove that the parallelogram, inscribed in a circle, is a rectangle.
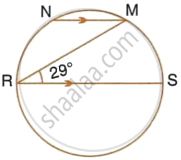
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
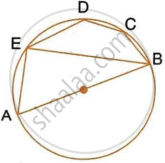
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate:
- ∠DAB,
- ∠DBA,
- ∠DBC,
- ∠ADC.
Also, show that the ΔAOD is an equilateral triangle.
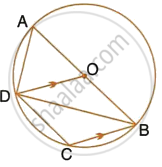
In the figure, ∠DBC = 58°. BD is diameter of the circle.
Calculate:
- ∠BDC
- ∠BEC
- ∠BAC