Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

उत्तर

i. ∠DAB = ∠BED = 65°
(Angle subtended by the same chord on the circle are equal)
ii. ∠ADB = 90°
(Angle in a semicircle is a right angle)
∴ ∠ABD = 90° – ∠DAB = 90° – 65° = 25°
AB || DC
∴ ∠BDC = ∠ABD = 25° (Alternate angles)
APPEARS IN
संबंधित प्रश्न
In the figure, m∠DBC = 58°. BD is the diameter of the circle. Calculate:
1) m∠BDC
2) m∠BEC
3) m∠BAC
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
In the figure, given below, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, fins the distance MN between the two chords of lengths 24 cm and 18 cm respectively.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBC
Also, show that the ΔAOD is an equilateral triangle.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠ADC
Also, show that the ΔAOD is an equilateral triangle.
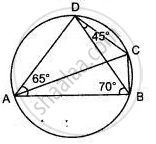
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.