Advertisements
Advertisements
प्रश्न
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠ADC
Also, show that the ΔAOD is an equilateral triangle.
उत्तर
∠ABD + ∠DBC = 30° + 30° = 60°
`=>` ∠ABC = 60°
In cyclic quadrilateral ABCD,
∠ADC + ∠ABC = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` ∠ADC = 180° – 60° = 120°
In ∆AOD, OA = OD (Radii of the same circle)
∠AOD = ∠DAO Or ∠DAB = 60° [Proved in (i)]
∠AOD = 60°
`=>` ∠ADO = ∠AOD = ∠DAO = 60°
∴ ∆AOD is an equilateral triangle.
APPEARS IN
संबंधित प्रश्न
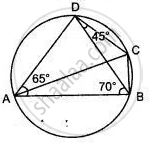
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Calculate the area of the shaded region, if the diameter of the semicircle is equal to 14 cm. Take `pi = 22/7`

Prove that the parallelogram, inscribed in a circle, is a rectangle.
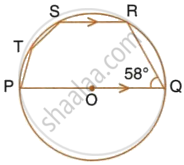
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°,
Calculate:
- ∠RPQ,
- ∠STP.
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.
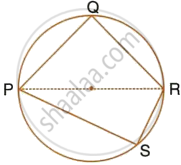
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
Using ruler and a compass only construct a semi-circle with diameter BC = 7cm. Locate a point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.