Advertisements
Advertisements
प्रश्न
उत्तर
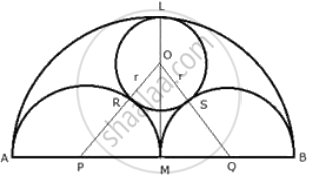
Let O, P and Q be the centers of the circle and semicircle.
Join OP and OQ.
OR = OS = r
And `AP = PM = MQ = QB = (AB)/4`
Now, `OP = OR + RP = r + (AB)/4` ...(Since PM = RP = radii of same circle)
Similarly, `OQ = OS + SQ = r + (AB)/4`
`OM = LM - OL = (AB)/2 - r`
Now in right ΔOPM,
OP2 = PM2 + OM2
`=> (r + (AB)/4)^2 = ((AB)/4)^2 + ((AB)/2 - r)^2`
`=> r^2 + (AB^2)/16 + (rAB)/2 = (AB^2)/16 + (AB^2)/4 + r^2 - rAB`
`=> (rAB)/2 = (AB^2)/4 - rAB`
`=> (AB^2)/4 = (rAB)/2 + rAB`
`=> (AB^2)/4 = (3rAB)/2`
`=> (AB)/4 = 3/2 r`
`=> AB = 3/2 rxx 4 = 6r`
Hence AB = 6 × r
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Prove that the parallelogram, inscribed in a circle, is a rectangle.
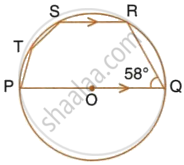
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°,
Calculate:
- ∠RPQ,
- ∠STP.
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
Using ruler and a compass only construct a semi-circle with diameter BC = 7cm. Locate a point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBC
Also, show that the ΔAOD is an equilateral triangle.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠ADC
Also, show that the ΔAOD is an equilateral triangle.
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
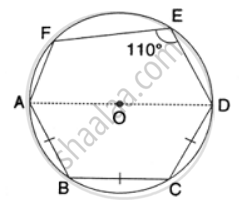
In the figure given alongside, AD is the diameter of the circle. If ∠ BCD = 130°, Calculate: (i) ∠ DAB (ii) ∠ ADB.
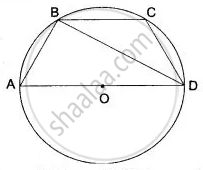
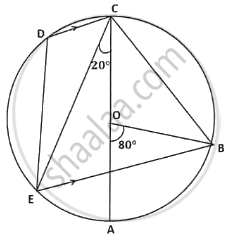
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED