Advertisements
Advertisements
प्रश्न
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

उत्तर
i. Since PAT || BC
∴ ∠PAB = ∠ABC (Alternate angles) ...(i)
In cyclic quadrilateral ABCD,
Ext ∠ADQ = ∠ABC ...(ii)
From (i) and (ii)
∠PAB = ∠ADQ
ii. Arc AB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
∴ ∠AOB = 2∠ADB
`=>` ∠AOB = 2∠PAB ...(Angles in alternate segments)
`=>` ∠AOB = 2∠ADQ ...(Proved in (i) part)
iii. ∴ ∠BAP = ∠ADB ...(Angles in alternate segments)
But ∠BAP = ∠ADQ ...(Proved in (i) part)
∴ ∠ADQ = ∠ADB
APPEARS IN
संबंधित प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
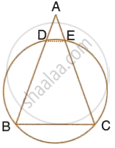
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
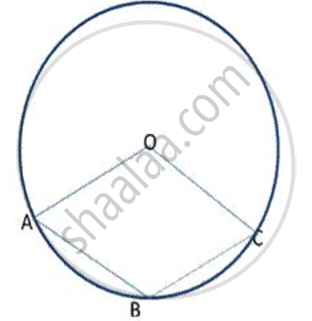
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
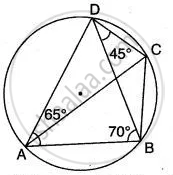
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.