Advertisements
Advertisements
प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

उत्तर

i. ∠BCD + ∠BAD = 180°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
`=>` ∠BCD = 180° – 105° = 75°
ii. Now, AB || CD
∴ ∠BAD + ∠ADC = 180°
(Interior angles on the same side of parallel lines is 180°)
`=>` ∠ADC = 180° – 105° = 75°
iii. ∠ADC + ∠ABC = 180°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
`=>` ∠ABC = 180° – 75° = 105°
APPEARS IN
संबंधित प्रश्न
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
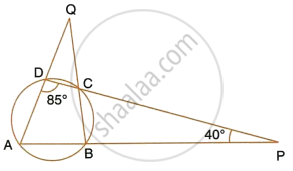
Use the given figure to find:
- ∠BAD,
- ∠DQB.
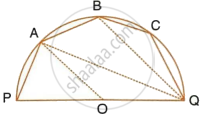
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
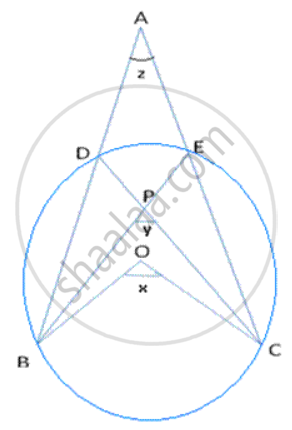
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
In following fig., O is the centre of the circle. Find ∠ CBD.
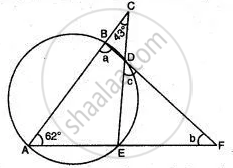
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.