Advertisements
Advertisements
प्रश्न
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.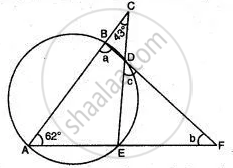
उत्तर
ABCE is cyclic quadrilateral.
∴ ∠ ABD + ∠ AED = 180°
and ∠ EAB + ∠ BDE = 180°
Now in Δ ACE
∠ A + ∠ C + ∠ E = 180°
62° + 43° + ∠ E = 180°
∠ E = 180° - 105° = 75°
So,
∠ ABD + ∠ AED = 180°
∴ a + 75° = 180°
∴ a = 105°
∠ EDF = ∠ BAE ....(Exterior angle of cyclic quadrilateral)
∴ 62° = c
∴ c = 62°
In Δ ABF,
∠ ABF + ∠BAF + ∠BFA = 180°
∴ 105° + 62° + b = 180°
∴ 167° + b = 180°
∴ b = 180° - 167°
∴ b = 13°
a = 105°, b = 13° and c = 62°
APPEARS IN
संबंधित प्रश्न
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
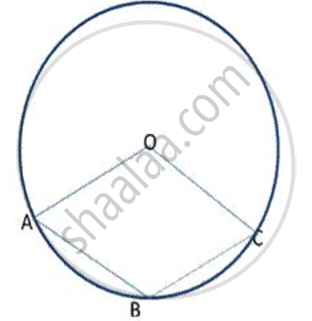
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
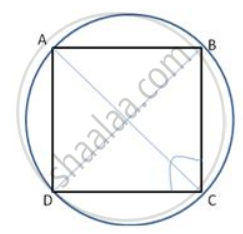
In the following figure, Prove that AD is parallel to FE.

ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
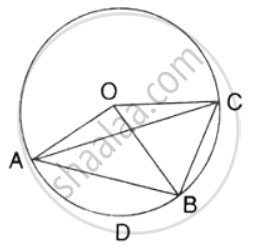
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
