Advertisements
Advertisements
Question
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.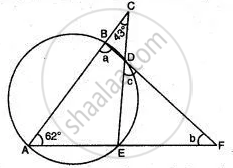
Solution
ABCE is cyclic quadrilateral.
∴ ∠ ABD + ∠ AED = 180°
and ∠ EAB + ∠ BDE = 180°
Now in Δ ACE
∠ A + ∠ C + ∠ E = 180°
62° + 43° + ∠ E = 180°
∠ E = 180° - 105° = 75°
So,
∠ ABD + ∠ AED = 180°
∴ a + 75° = 180°
∴ a = 105°
∠ EDF = ∠ BAE ....(Exterior angle of cyclic quadrilateral)
∴ 62° = c
∴ c = 62°
In Δ ABF,
∠ ABF + ∠BAF + ∠BFA = 180°
∴ 105° + 62° + b = 180°
∴ 167° + b = 180°
∴ b = 180° - 167°
∴ b = 13°
a = 105°, b = 13° and c = 62°
APPEARS IN
RELATED QUESTIONS
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

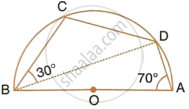
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
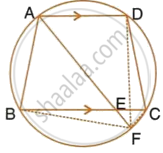
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC