Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
Solution
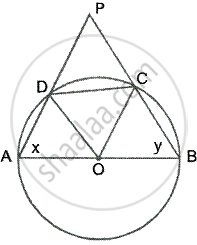
In a circle, ABCD is a cyclic quadrilateral in which AB is the diameter and chord CD is equal to the radius of the circle
To prove – ∠APB = 60°
Construction – Join OC and OD
Proof – Since chord CD = CO = DO ...[Radii of the circle]
∴ ΔDOC is an equilateral triangle
∴ ∠DOC = ∠ODC = ∠DCO = 60°
Let ∠A = x and ∠B = y
Since OA = OB = OC = OD ...[Radii of the same circle]
∴ ∠ODA = ∠OAD = x and ∠OCB = ∠OBC = y
∴ ∠AOD = 180° – 2x and ∠BOC = 180° – 2y
But AOB is a straight line
∴ ∠AOD + ∠BOC + ∠COD = 180°
`=>` 180° – 2x + 180° – 2y + 60° = 180°
`=>` 2x + 2y = 240°
`=>` x + y = 120°
But ∠A + ∠B + ∠P = 180° ...[Angles of a triangle]
`=>` 120° + ∠P = 180°
`=>` ∠P = 180° – 120°
`=>` ∠P = 60°
Hence ∠APB = 60°
APPEARS IN
RELATED QUESTIONS
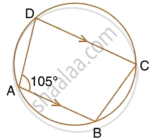
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
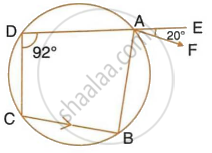
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
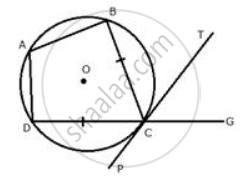
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In the figure, given below, find: ∠ADC, Show steps of your working.
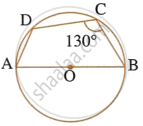
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
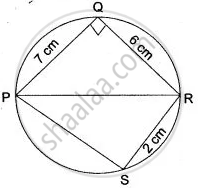
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.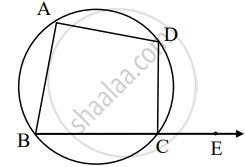
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
