Advertisements
Advertisements
Question
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
Solution
PQ is a diameter of the circle
∴ CPRQ = 90° (angle is a semi cirde)
∠ RPQ = 40° (given)
In Δ PQR,
∠ PRQ + ∠ RQP + ∠ QPR = 180 (Angle sum property)
90 + ∠ RQP + 40 = 180
∠ RQP = 50 °
APPEARS IN
RELATED QUESTIONS
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

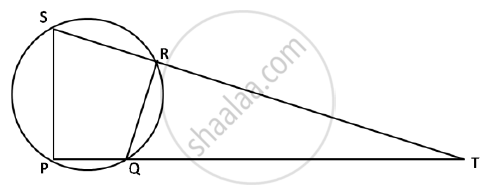
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
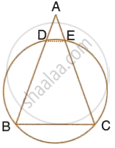
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
In following fig., O is the centre of the circle. Find ∠ CBD.
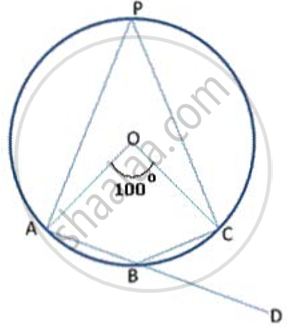
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
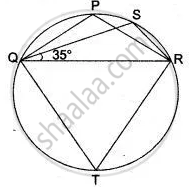
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.