Advertisements
Advertisements
प्रश्न
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
उत्तर
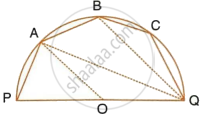
PQ is a diameter of the circle
∴ CPRQ = 90° (angle is a semi cirde)
∠ RPQ = 40° (given)
In Δ PQR,
∠ PRQ + ∠ RQP + ∠ QPR = 180 (Angle sum property)
90 + ∠ RQP + 40 = 180
∠ RQP = 50 °
APPEARS IN
संबंधित प्रश्न
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
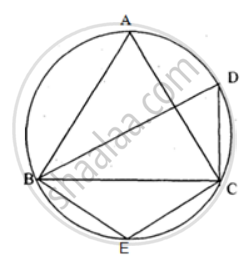
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
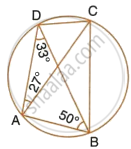
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
In the following figure, Prove that AD is parallel to FE.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
