Advertisements
Advertisements
प्रश्न
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

उत्तर
We know that angle by the same arc at circle i.e., on the circumference is half of the angle by the same arc at the center.
∵ ∠x = `1/2` x 160° = 80° ....(Opposite triangles of a cyclic quadrilateral supplementary)
∴ ∠x + ∠y = 180°
∴ ∠y = 100°
∴ 3∠y - 2∠x
= 3 x 100° - 2 x 80°
= 300° - 160°
= 140°.
APPEARS IN
संबंधित प्रश्न
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

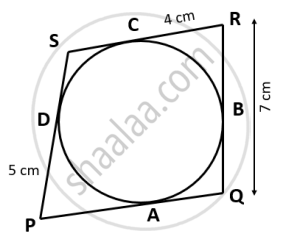
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
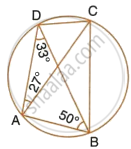
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
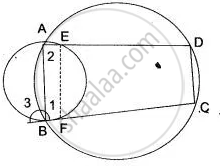
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: