Advertisements
Advertisements
प्रश्न
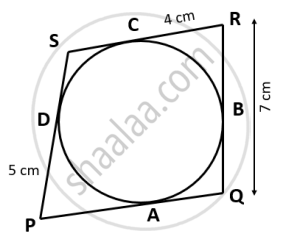
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ:
उत्तर
PD = PA = 5 cm ....(1) [Tangents from exterior point are equal in length]
QA = QB = q ....(2) [Tangents from exterior point are equal in length]
RC = RB = r = 4 cm ....(3) [Tangents from exterior point are equal in length]
SD = SC = s ....(4) [Tangents from exterior point are equal in length]
RQ = RB + BQ (given)
⇒ 7 cm = 4 + QB ...[from (3)]
⇒ QB = 3 cm ...(5)
∵ QA = QB = 3 cm ...(6) [from (2) and (5)]
∴ PQ = PA + AQ
∴ PQ = 5 + 3 ....[From (1) and (6)]
∴ PQ = 8 cm
APPEARS IN
संबंधित प्रश्न
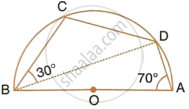
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
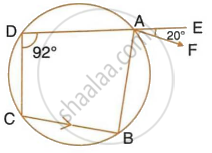
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
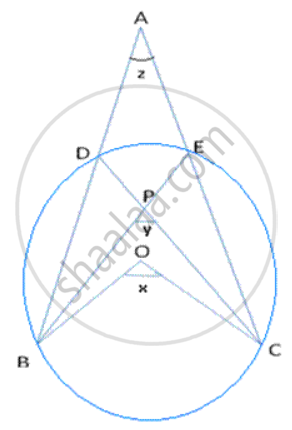
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
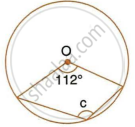
In the following figure, O is the centre of the circle. Find the values of a, b and c.
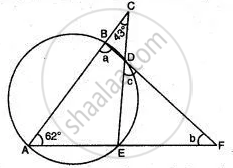
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.