Advertisements
Advertisements
Question
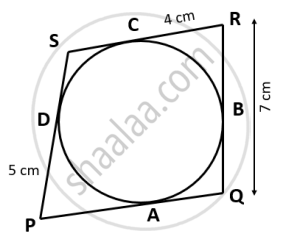
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ:
Solution
PD = PA = 5 cm ....(1) [Tangents from exterior point are equal in length]
QA = QB = q ....(2) [Tangents from exterior point are equal in length]
RC = RB = r = 4 cm ....(3) [Tangents from exterior point are equal in length]
SD = SC = s ....(4) [Tangents from exterior point are equal in length]
RQ = RB + BQ (given)
⇒ 7 cm = 4 + QB ...[from (3)]
⇒ QB = 3 cm ...(5)
∵ QA = QB = 3 cm ...(6) [from (2) and (5)]
∴ PQ = PA + AQ
∴ PQ = 5 + 3 ....[From (1) and (6)]
∴ PQ = 8 cm
APPEARS IN
RELATED QUESTIONS
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

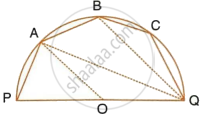
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
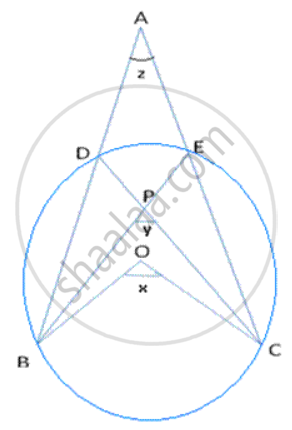
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.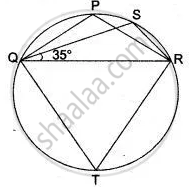
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.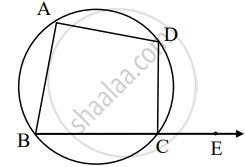
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
