Advertisements
Advertisements
Question
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

Solution
Given: PQRS is a cyclic quadrilateral.
∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°
1) Opposite angle of a cyclic quadrilateral is supplementary.
⇒ ∠QPS + ∠QRS = 180°
⇒ 73° + ∠QRS = 180°
⇒ ∠QRS = 180° - 73= 107°
2) Opposite angle of a cyclic quadrilateral are supplementary.
⇒ ∠PSR + ∠PQR = 180°
⇒ ∠PSR + (⇒ ∠PQS + ⇒ ∠RQS) = 180°
⇒ 82° + 55° + ∠RQS = 180°
⇒ ∠RQS = 180° - 137° = 43°
3) In ΔPQS, by angle sum property, we have
⇒ ∠PSQ + ∠PQS + ∠QPS = 180°
⇒ ∠PSQ + 55° + 73° = 180°
⇒ ∠PSQ = 180° - 128° = 52°
Now ⇒ ∠PRQ = ∠PSQ (angles in the same segment of a circle)
⇒ ∠PRQ = 52°
APPEARS IN
RELATED QUESTIONS
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
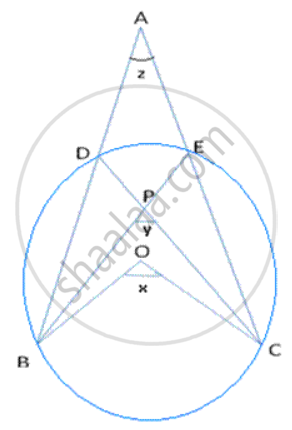
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
In the figure, given below, find: ∠ABC. Show steps of your working.

Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
