Advertisements
Advertisements
Question
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
Solution
Here, ABCD is a cyclic quadrilateral.
PM is the bisector of ∠ APB and QM is a bisector of ∠ AQD.
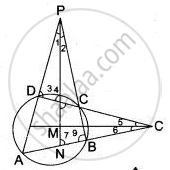
In Δ PDL and Δ PBN,
∠ 1 = ∠ 2 ...( PM is the bisector of ∠P )
∠ 3 = ∠ 9 ...( Exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.)
∠ 4 = ∠ 7
But, ∠ 4 = ∠ 8 ...( Vertically opposite angles)
∠ 7 = ∠ 8
Now in Δ QMN and Δ QML,
∠ 7 = ∠ 8 ...(prove above)
∠ 5 = ∠ 6 ...( QM is a bisector of Q)
Δ QMN ∼ Δ QML
∠ QMN = ∠ QML
But
∠ QMN + ∠ QML = 180°
∠ QMN = ∠ QML = 90°
Hence, ΔPMQ = 90° ...( ∵ ∠PMQ = ∠QML)
Hence proved.
APPEARS IN
RELATED QUESTIONS
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
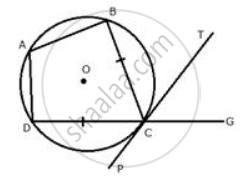
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
In the figure, given below, find: ∠ABC. Show steps of your working.

The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
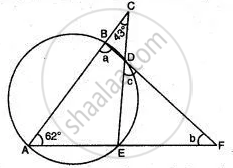
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.