Advertisements
Advertisements
Question
In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD.
Solution 1
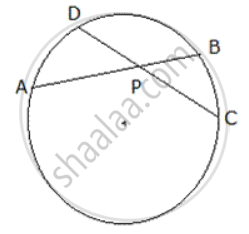
If two chords of a circle interest internally then the products of the lengths of segments are equal, then
AP x BP= CP x DP ... ( 1)
But, AP= CP (Given) ....(2)
Then from ( 1) and (2), we have
BP= DP ......(3)
Adding (2) and (3),
AP + BP= CP + DP
⇒ AB = CD
Hence Proved.
Solution 2
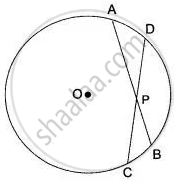
In order to prove the desired result, we shall first prove that ΔPAD ∼ ΔPCB.
In triangles PAD and PCB, we have:
∠ PAD = ∠PCB ...[Angles in the same segment of arc BD]
∠ APD = ∠ CPB ...[Vertically opposite angles]
So, by AAA criterion of similarity, we have
ΔPAD ∼ ΔPCB.
⇒ `"PA"/"PC" = "PD"/"PB"` ....[Corresponding sides of similar triangles are in the same ratio]
⇒ `"AP"/"CP" = "PD"/"PB"`
⇒ 1 = `"PD"/"PB" ...[ ∴ "AP" = "CP", "AP"/"CP" = 1]`
⇒ PB = PD
⇒ AP + PB = AP + PD ....[ Adding AP on both sides ]
⇒ AP + PB = CP + PD ...[ ∵AP = CP ]
⇒ AB = CD.
Hence proved.
RELATED QUESTIONS
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
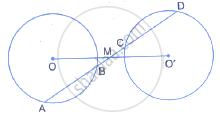
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN = ∠DNM.
(ii) ∠AMN = ∠CNM.
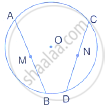
Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle, prove that:
(i) AP = CP,
(ii) BP = DP
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the area of the rhombus is `32sqrt(3) cm^2` find the radius of the circle.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
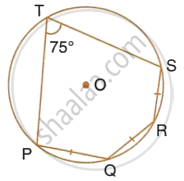
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
- ∠POS,
- ∠QOR,
- ∠PQR.
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP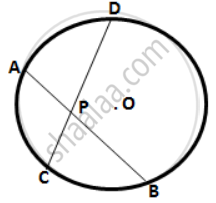
Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB
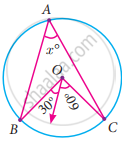
Find the value of x° in the following figure: