ICSE solutions for Mathematics [English] Class 10 chapter 15 - Circles [Latest edition]

If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.

If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.

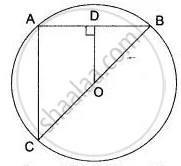
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.

In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.

In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.

In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC. 

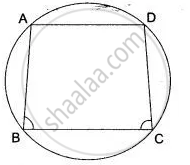
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.

Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.

Two circles are drawn with sides AB, AC of a triangle ABC as diameters. They intersect at a point D. Prove that D lies on BC.

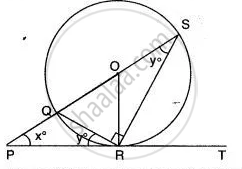
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°

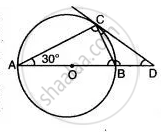
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.

Prove that the line segment joining the midpoints of two equal chords of a circle subtends equal angles with the chord.

In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.

In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD. 

Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.

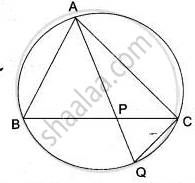
In the given Figure. P is any point on the chord BC of a circle such that AB = AP. Prove that CP = CQ.

The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.

In a circle with center O, chords AB and CD intersect inside the circumference at E. Prove that ∠ AOC + ∠ BOD = 2∠ AEC.

In the given Figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is the radius of the circumcircle of A ABC, whose center is O.

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. 

In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.

If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A. 

If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.

Two circle with radii r₁ and r₂ touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.

If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.

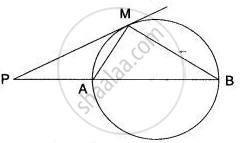
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB²

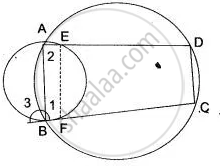
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

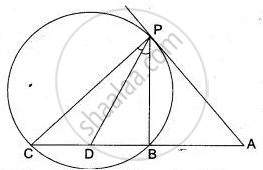
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).

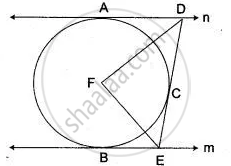
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°

A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.

Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.

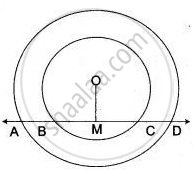
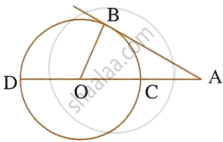
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.

In the given circle with diameter AB, find the value of x.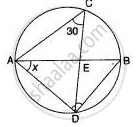

In the given figure, the area enclosed between the two concentric circles is 770 cm². If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.

Two chords AB and CD of a circle are parallel and a line L is the perpendicular bisector of AB. Show that L bisects CD.

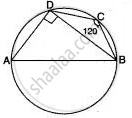
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA

Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.

The radius of a circle is 13 cm and the length of one of its chord is 10 cm. Find the distance of the chord from the centre.

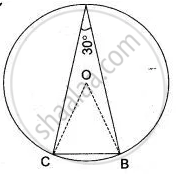
C is a point on the minor arc AB of the circle, with centre O. Given ∠ACB = x° and ∠AOB = y° express y in terms of x. Calculate x, if ACBO is a parallelogram.

AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.

AB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠ BAD and ∠ ACD.

In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD,  (ii) ∠ ADB.
Hence show that AC is a diameter.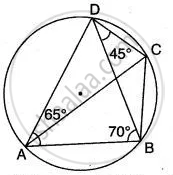

In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT). 

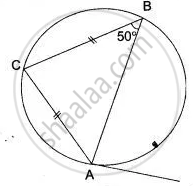
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.

In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.

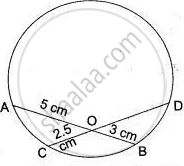
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.

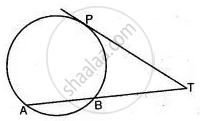
In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.

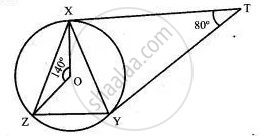
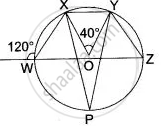
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.

A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.

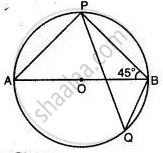
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.

Two chords AB, CD of lengths 16 cm and 30 cm, are parallel. If the distance between AB and CD is 23 cm. Find the radius of the circle.

Two circles of radii 10 cm and 8 cm intersect and the length of the common chord is 12 cm. Find the distance between their centres.

AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.

In Fig. O is the centre of the circle with radius 5 cm. OP⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.

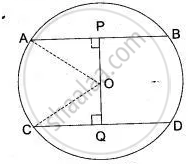
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.

In Fig. O is the centre of the circle of radius 5 cm. OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 6 cm and CD = 8 cm. Determine PQ.

In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the 
(i) radius of the circle
(ii) length of chord CD.

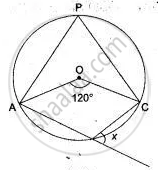
If O is the centre of the circle, find the value of x in each of the following figures

If O is the centre of the circle, find the value of x in each of the following figures

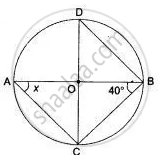
If O is the centre of the circle, find the value of x in each of the following figures

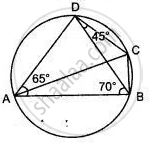
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.

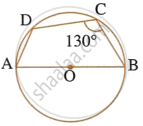
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:

1. ∠DAB
2. ∠DBA

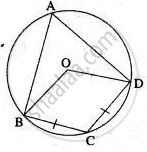
 In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.

In the given below the figure, AB is parallel to DC, ∠BCD = 80° and ∠BAC = 25°, Find 
(i) ∠CAD, (ii) ∠CBD, (iii) ∠ADC.

In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.

In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.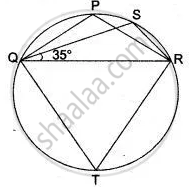

In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.

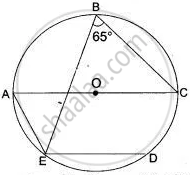
In the figure, ∠DBC = 58°. BD is diameter of the circle.

Calculate:

1. ∠BDC
2. ∠BEC
3. ∠BAC

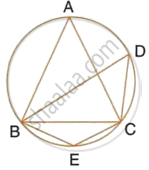
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:

1. ∠CBA
2. ∠CQB

In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

P and Q are the centre of circles of radius 9 cm and 2 cm respectively; PQ = 17 cm. R is the centre of circle of radius x cm, which touches the above circles externally, given that ∠ PRQ = 90°. Write an equation in x and solve it.

In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate: 
(i) ∠ AQP,      (ii) ∠ BQP
(iii) ∠ AQB,    (iv) ∠ APB
(v) ∠ AOB,     (vi) ∠ ATB

In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.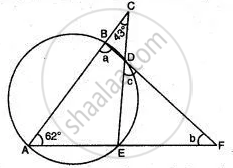

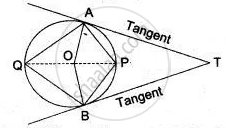
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB

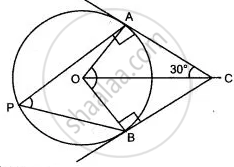
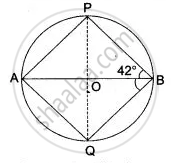
In the following figure, O is the centre of the circle, ∠ PBA = 42°.
Calculate:
(i) ∠ APB
(ii) ∠PQB
(iii) ∠ AQB

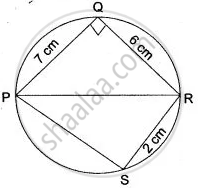
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.

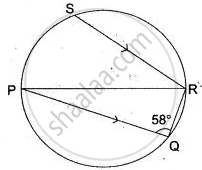
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)

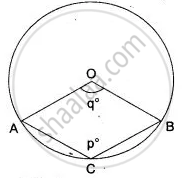
C is a point on the minor arc AB of the circle, with centre O. Given ∠ACB = p°, ∠AOB = q°.
(i) Express q in terms of p.
(ii) Calculate p if ACBO is a parallelogram. 
(iii) If ACBO is a parallelogram, then find the value of q + p.

AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.

In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC,   (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD

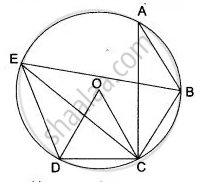
In the figure, AB = AC = CD, ∠ADC = 38°. Calculate: (i) ∠ ABC, (ii) ∠ BEC.

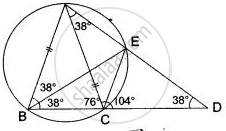
In the figure given alongside, AD is the diameter of the circle. If ∠ BCD = 130°, Calculate: (i) ∠ DAB (ii) ∠ ADB.

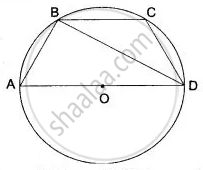
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.

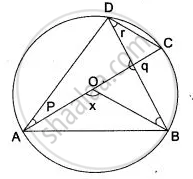
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.

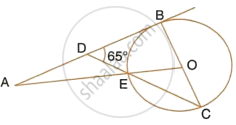
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:

1. AB.
2. the length of tangent PT.

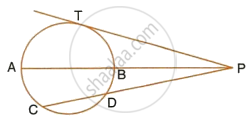
In the figure alongside O is the centre of circle ∠ XOY = 40°, ∠ TWX = 40° and XY is parallel to TZ.
Find: (i) ∠ XZY, (ii) ∠ YXZ (iii) ∠ TZY.

In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

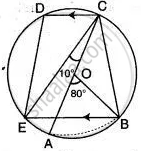
In the diagram given alongside, AC is the diameter of the circle, with centre O. CD and BE are parallel. ∠ AOB = 80° and ∠ ACE = 10°. Calculate: (i) ∠ BEC (ii) ∠ BCD (iii) ∠ CED.