Advertisements
Advertisements
Question
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
Solution
AB = 24 cm, OM = 5 cm, ON = 12 cm.
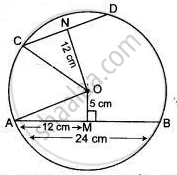
(i) In Δ AOM,
OA2 = OM2 + AM2
OA2 = 52 + 122
OA2 = 25 + 144 = 169
OA = 13 cm.
Thus, radius of the circle is 13 cm.
(ii) In Δ CON,
OC2 = ON2 + CN2
132 = 122 + CN2 ....( ∵ OC = OA = 13 (Radius))
169 - 144 = CN2
CN2 = 25
CN = 5.
Thus length of chord CD = 2CN = 2 x 5 = 10 cm
APPEARS IN
RELATED QUESTIONS
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of the circle.
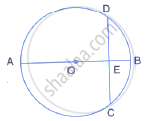
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
The figure shows two concentric circles and AD is a chord of larger circle.
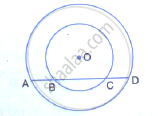
Prove that: AB = CD
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
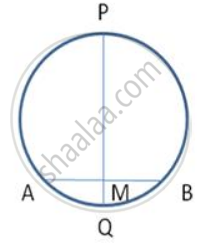
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y : express ∠ABD in terms of y.

A chord of length 6 cm is drawn in a circle of radius 5 cm.
Calculate its distance from the center of the circle.
A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the center.
In the following figure, AD is a straight line, OP ⊥ AD and O is the centre of both circles. If OA = 34cm, OB = 20 cm and OP = 16 cm;
find the length of AB.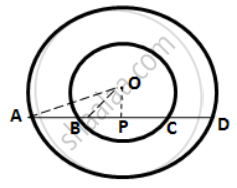
AB and CD are two equal chords of a circle with center O which intersect each other at a right angle at point P.
If OM ⊥ AB and ON ⊥ CD;
show that OMPN is a square.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
