Advertisements
Advertisements
Question
AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
Solution
(i) AC = `Sqrt((3 + 2)^2 + (-7 - 5)^2)` ...(Distance Formula)
= `sqrt( 25 + 144)`
Radius = `sqrt169` = 13 units

(ii) As 'c' is midpoint of AB
`-2 = (3 + x)/2` ...(midpoint theorem)
or - 4 = 3 + x
x = - 7
and 5 = `(- 7 + y)/2`
and 10 = - 7 + y
and y = 17
∴ B(-7, 17)
APPEARS IN
RELATED QUESTIONS
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its centre to a chord is 8.0 cm. Calculate the length of the chord.
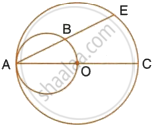
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
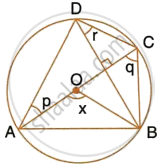
In the given figure, AC is a diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.
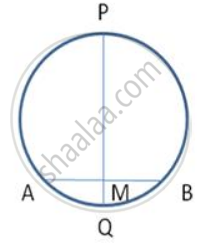
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
OP is the ⊥ bisector of chord AB.
The radius of a circle is 17.0 cm and the length of the perpendicular drawn from its center to a chord is 8.0 cm.
Calculate the length of the chord.
A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the center.
In the following figure, AD is a straight line, OP ⊥ AD and O is the centre of both circles. If OA = 34cm, OB = 20 cm and OP = 16 cm;
find the length of AB.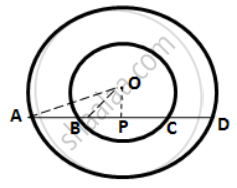
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
