Advertisements
Advertisements
प्रश्न
AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
उत्तर
(i) AC = `Sqrt((3 + 2)^2 + (-7 - 5)^2)` ...(Distance Formula)
= `sqrt( 25 + 144)`
Radius = `sqrt169` = 13 units

(ii) As 'c' is midpoint of AB
`-2 = (3 + x)/2` ...(midpoint theorem)
or - 4 = 3 + x
x = - 7
and 5 = `(- 7 + y)/2`
and 10 = - 7 + y
and y = 17
∴ B(-7, 17)
APPEARS IN
संबंधित प्रश्न
AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the
radius of the circle is 13 cm. find the distance between the two chords.

A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are
(i) on the opposite sides of the centre,
(ii) on the same side of the centre.
A chord CD of a circle whose centre is O, is bisected at P by a diameter AB.
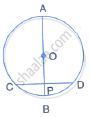
Given OA = OB = 15 cm and OP = 9 cm. calculate the length of:
(i) CD (ii) AD (iii) CB
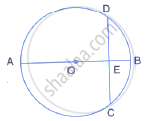
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
The figure shows two concentric circles and AD is a chord of larger circle.
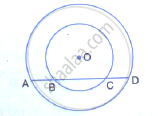
Prove that: AB = CD
A chord of length 6 cm is drawn in a circle of radius 5 cm.
Calculate its distance from the center of the circle.
The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
The radius of a circle is 13 cm and the length of one of its chords is 24 cm.
Find the distance of the chord from the center.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
