Advertisements
Advertisements
प्रश्न
AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
उत्तर
(i) AC = `Sqrt((3 + 2)^2 + (-7 - 5)^2)` ...(Distance Formula)
= `sqrt( 25 + 144)`
Radius = `sqrt169` = 13 units

(ii) As 'c' is midpoint of AB
`-2 = (3 + x)/2` ...(midpoint theorem)
or - 4 = 3 + x
x = - 7
and 5 = `(- 7 + y)/2`
and 10 = - 7 + y
and y = 17
∴ B(-7, 17)
APPEARS IN
संबंधित प्रश्न
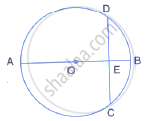
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
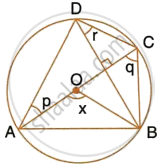
In the given figure, AC is a diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
AB and CD are two equal chords of a circle with center O which intersect each other at a right angle at point P.
If OM ⊥ AB and ON ⊥ CD;
show that OMPN is a square.
The radius of a circle is 13 cm and the length of one of its chords is 24 cm.
Find the distance of the chord from the center.
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB. If AB = 32 cm,
find the length of CD.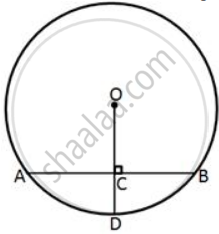
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.
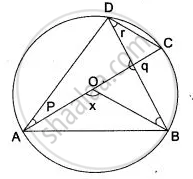
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
