Advertisements
Advertisements
प्रश्न
AB and CD are two equal chords of a circle with center O which intersect each other at a right angle at point P.
If OM ⊥ AB and ON ⊥ CD;
show that OMPN is a square.
उत्तर
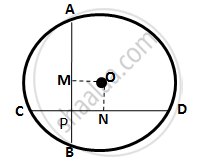
Clearly , all the angles of OMPN are 90°.
OM ⊥ AB and ON ⊥ CD
∴ BM = `1/2"AB" = 1/2`CD = CN ....(i) ...[ perpendicular drawn from the center of a circle to a chord bisects it ]
As the two equal chords, AB and CD intersect at point P inside the circle,
∴ AP = DP and CP = BP .....(ii)
Now, CN - CP = BM - BP ...[ by (i) and (ii) ]
⇒ PN = MP
∴ Quadrilateral OMPN is A square.
APPEARS IN
संबंधित प्रश्न
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of the circle.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are
(i) on the opposite sides of the centre,
(ii) on the same side of the centre.
A chord CD of a circle whose centre is O, is bisected at P by a diameter AB.
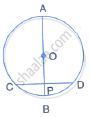
Given OA = OB = 15 cm and OP = 9 cm. calculate the length of:
(i) CD (ii) AD (iii) CB
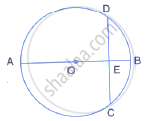
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
The figure shows two concentric circles and AD is a chord of larger circle.
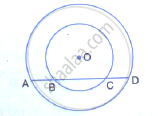
Prove that: AB = CD
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of
the circles. Show that:
(i) AB = CD,
(ii) AC = BD.

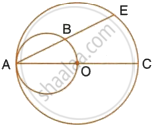
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y : express ∠ABD in terms of y.

Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively.
Calculate the distance between the chords, if they are on:
(i) the same side of the center.
(ii) the opposite sides of the center.
