Advertisements
Advertisements
प्रश्न
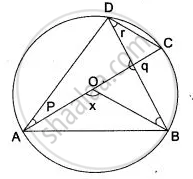
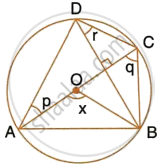
In the given figure, AC is a diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.
उत्तर

∵ Arc subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB
But ∠ADB and ∠ACB are in the same segment
∴ ∠ADB = ∠ACB = q
Now in ΔAED.
p + q + 90° = 180° ...(Sum of angles of a Δ)
p + q = 90°
p = 90° – q
∵ Arc BC subtends ∠BOC at the centre and ∠ADC at the remaining part of the circle
∴ ∠BOC = 2∠BDC = 2r
∴
∵ (∠AOB + ∠BOC = 180°)
∴
=
APPEARS IN
संबंधित प्रश्न
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are
(i) on the opposite sides of the centre,
(ii) on the same side of the centre.
Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
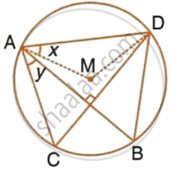
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠MAD = x and ∠BAC = y :
- express ∠AMD in terms of x.
- express ∠ABD in terms of y.
- prove that : x = y.
In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm, 
Find the :
(i) the radius of the circle
(ii) length of chord CD.
In the following figure; P and Q are the points of intersection of two circles with centers O and O'. If straight lines APB and CQD are parallel to OO';
prove that: (i) OO' = 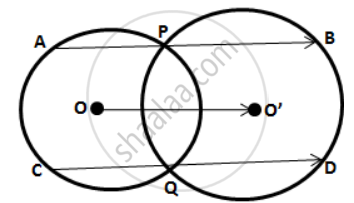
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively.
Calculate the distance between the chords, if they are on:
(i) the same side of the center.
(ii) the opposite sides of the center.
Two chords AB and CD of a circle are parallel and a line L is the perpendicular bisector of AB. Show that L bisects CD.
The radius of a circle is 13 cm and the length of one of its chord is 10 cm. Find the distance of the chord from the centre.
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.