Advertisements
Advertisements
प्रश्न
In the following figure; P and Q are the points of intersection of two circles with centers O and O'. If straight lines APB and CQD are parallel to OO';
prove that: (i) OO' = `1/2`AB ; (ii) AB = CD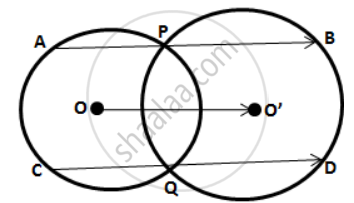
उत्तर
Drop OM and O'N perpendicular on AB and OM' and O'N' perpendicular on CD.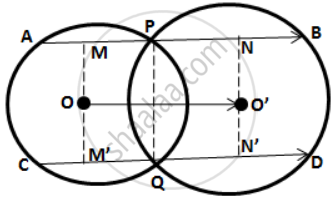
∴ OM, O'N, OM' and O'N' bisect AP, PB, CQ and QD respectively.
( Perpendicular is drawn from the center of a circle to a chord bisects it. )
∴ MP = `1/2"AP" , "PN" = 1/2"BP" , "M'Q" = 1/2"CQ" , "QN"' = 1/2"QD"`
Now, OO' = MN = MP + PN = `1/2( "AP + BP" ) = 1/2"AB"` ...(i)
and OO' = M'N' = M'Q + QN' = `1/2( "CQ + QD" ) = 1/2"CD"` ...(ii)
By (i) and (ii),
AB = CD.
APPEARS IN
संबंधित प्रश्न
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
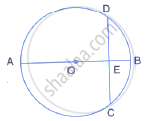
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of
the circles. Show that:
(i) AB = CD,
(ii) AC = BD.

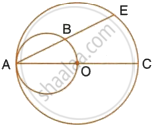
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
In Δ ABC, the perpendicular from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively. Prove that: arc CD = arc CE
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm, 
Find the :
(i) the radius of the circle
(ii) length of chord CD.
The radius of a circle is 17.0 cm and the length of the perpendicular drawn from its center to a chord is 8.0 cm.
Calculate the length of the chord.
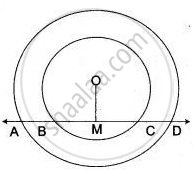
In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.
AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
