Advertisements
Advertisements
Question
In the following figure; P and Q are the points of intersection of two circles with centers O and O'. If straight lines APB and CQD are parallel to OO';
prove that: (i) OO' = `1/2`AB ; (ii) AB = CD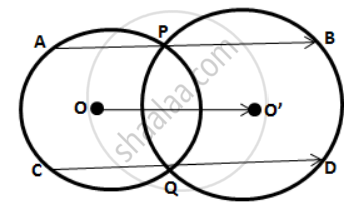
Solution
Drop OM and O'N perpendicular on AB and OM' and O'N' perpendicular on CD.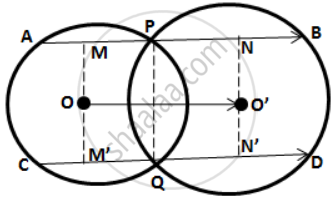
∴ OM, O'N, OM' and O'N' bisect AP, PB, CQ and QD respectively.
( Perpendicular is drawn from the center of a circle to a chord bisects it. )
∴ MP = `1/2"AP" , "PN" = 1/2"BP" , "M'Q" = 1/2"CQ" , "QN"' = 1/2"QD"`
Now, OO' = MN = MP + PN = `1/2( "AP + BP" ) = 1/2"AB"` ...(i)
and OO' = M'N' = M'Q + QN' = `1/2( "CQ + QD" ) = 1/2"CD"` ...(ii)
By (i) and (ii),
AB = CD.
APPEARS IN
RELATED QUESTIONS
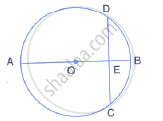
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
A chord of length 8 cm is drawn at a distance of 3 cm from the center of the circle.
Calculate the radius of the circle.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords,
if both the chords are:
(i) on the opposite sides of the centre;
(ii) on the same side of the centre.
In the following figure, AD is a straight line, OP ⊥ AD and O is the centre of both circles. If OA = 34cm, OB = 20 cm and OP = 16 cm;
find the length of AB.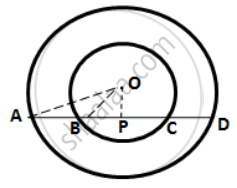
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.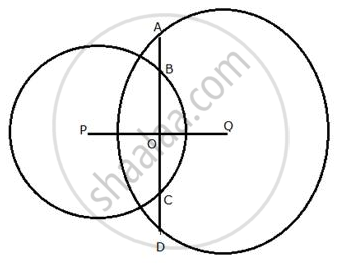
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB. If AB = 32 cm,
find the length of CD.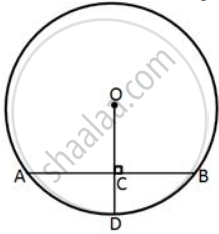
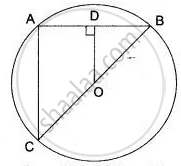
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
