Advertisements
Advertisements
Question
M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O.
Prove that: (i) ∠BMN = ∠DNM
(ii) ∠AMN = ∠CNM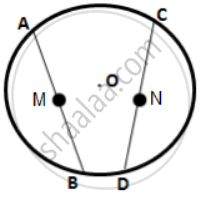
Solution
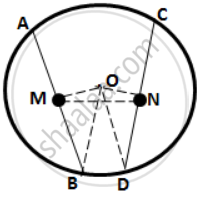
Drop OM ⊥ AB and ON ⊥ CD.
∴ OM bisects AB and ON bisects CD. ...( Perpendicular drawn from the centre of a circle to a chord bisects it. )
⇒ BM = `1/2"AB" = 1/2"CD"` = DN ....(1)
Applying Pythagoras theorem,
OM2 = OB2 - BM2
= OD2 - DN2 ....( By 1 )
= ON2
∴ OM = ON
⇒ ∠OMN = ∠ONM ....(2)
( Angles opp to equal sides are equal. )
(i) ∠OMB = ∠OND .....( both 90° )
Subtracting (2) from above,
∠BMN = ∠DNM
(ii) ∠OMA = ∠ONC .....( both 90° )
Adding (2) to above,
∠AMN = ∠CNM.
APPEARS IN
RELATED QUESTIONS
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of the circle.
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC.
A chord of length 8cm is drawn inside a circle of radius 6cm. Find the perpendicular distance of the chord from the centre of the circle.
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm, 
Find the :
(i) the radius of the circle
(ii) length of chord CD.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords,
if both the chords are:
(i) on the opposite sides of the centre;
(ii) on the same side of the centre.
A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the center.
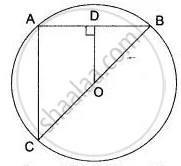
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
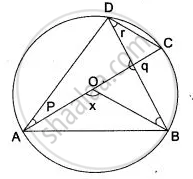
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
