Advertisements
Advertisements
Question
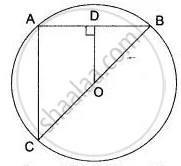
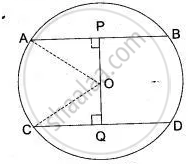
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
Solution
Since OD ⊥ AB and the perpendicular drawn from the centre to a chord bisects the chord.
∴ D is the midpoint of AB.
Also, O being the center is the midpoint of BC.
Thus, in Δ ABC, D and O are the midpoint of AB and BC respectively.
Therefore, OD || AC
and OD = `1/2`CA ....[ ∵ Segment joining the midpoints of two sides of a triangle is half of the third side ]
⇒ CA = 2OD ...Hence proved.
APPEARS IN
RELATED QUESTIONS
A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
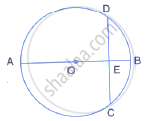
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of
the circles. Show that:
(i) AB = CD,
(ii) AC = BD.

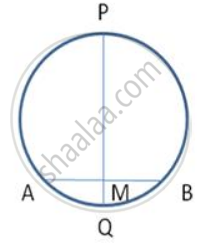
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y : express ∠ABD in terms of y.

The radius of a circle is 17.0 cm and the length of the perpendicular drawn from its center to a chord is 8.0 cm.
Calculate the length of the chord.
M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O.
Prove that: (i) ∠BMN = ∠DNM
(ii) ∠AMN = ∠CNM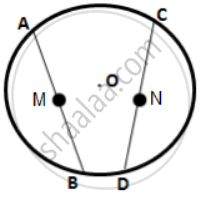
In Fig. O is the centre of the circle with radius 5 cm. OP⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
