Advertisements
Advertisements
Question
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
Solution
Let O be the centre of the given circle and let it's radius be r cm. Draw OP ⊥ AB and OQ ⊥ CD.
Since AB || CD. Therefore, points P, O and Q are collinear. So, PQ = 17 cm.

Let Op = x cm. Then, OQ = (17 - x) cm
Join OA and OC. Then, OA = OC = r.
Since, the perpendicular from the centre to a chord of the circle bisects the chord.
∴ AP = PB = 5 cm and CQ = QD = 12 cm.
In right triangles OAP and OCQ, we have
OA2 = OP2 + AP2 and OC2 = OQ2 + CQ2
⇒ r2 = x2 + 52 ...(i)
and r2 = (17 - x)2 + 122 ....(ii)
⇒ x2 + 52 = (17 - x)2 + 122 ....(On equating the values of r2)
⇒ x2 + 25 = 289 - 34x + x2 + 144
⇒ 34x = 408
⇒ x = 12 cm
Putting x = 12 cm in (i), we get
r2 = 122 + 52 = 169
⇒ r = 13 cm
Hence, the radius of the circle is 13 cm.
APPEARS IN
RELATED QUESTIONS
A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its centre to a chord is 8.0 cm. Calculate the length of the chord.
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
The figure shows two concentric circles and AD is a chord of larger circle.
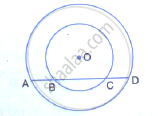
Prove that: AB = CD
The given figure shows two circles with centres A and B; and radii 5 cm and 3 cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

The radius of a circle is 17.0 cm and the length of the perpendicular drawn from its center to a chord is 8.0 cm.
Calculate the length of the chord.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords,
if both the chords are:
(i) on the opposite sides of the centre;
(ii) on the same side of the centre.
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively.
Calculate the distance between the chords, if they are on:
(i) the same side of the center.
(ii) the opposite sides of the center.
The radius of a circle is 13 cm and the length of one of its chord is 10 cm. Find the distance of the chord from the centre.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
