Advertisements
Advertisements
प्रश्न
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
उत्तर
Let O be the centre of the given circle and let it's radius be r cm. Draw OP ⊥ AB and OQ ⊥ CD.
Since AB || CD. Therefore, points P, O and Q are collinear. So, PQ = 17 cm.

Let Op = x cm. Then, OQ = (17 - x) cm
Join OA and OC. Then, OA = OC = r.
Since, the perpendicular from the centre to a chord of the circle bisects the chord.
∴ AP = PB = 5 cm and CQ = QD = 12 cm.
In right triangles OAP and OCQ, we have
OA2 = OP2 + AP2 and OC2 = OQ2 + CQ2
⇒ r2 = x2 + 52 ...(i)
and r2 = (17 - x)2 + 122 ....(ii)
⇒ x2 + 52 = (17 - x)2 + 122 ....(On equating the values of r2)
⇒ x2 + 25 = 289 - 34x + x2 + 144
⇒ 34x = 408
⇒ x = 12 cm
Putting x = 12 cm in (i), we get
r2 = 122 + 52 = 169
⇒ r = 13 cm
Hence, the radius of the circle is 13 cm.
APPEARS IN
संबंधित प्रश्न
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC.
Two chords of lengths 10cm and 24cm are drawn parallel o each other in a circle. If they are on the same side of the centre and the distance between them is 17cm, find the radius of the circle.
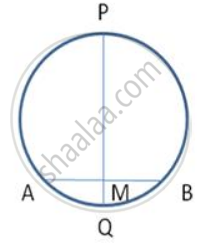
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
A chord CD of a circle whose center is O is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm.
Calculate the lengths of: (i) CD ; (ii) AD ; (iii) CB.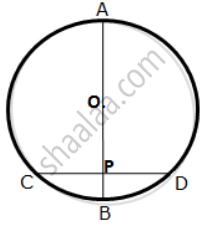
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
AB and CD are two equal chords of a circle with center O which intersect each other at a right angle at point P.
If OM ⊥ AB and ON ⊥ CD;
show that OMPN is a square.
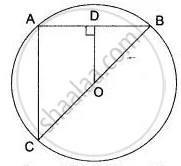
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
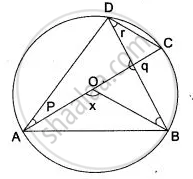
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.