Advertisements
Advertisements
प्रश्न
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
उत्तर
Since the distance between the chords is greater than the radius of the circle (15 cm), so the chords will be on the opposite sides of the center.
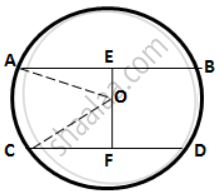
Let O be the center of the circle and AB and CD be the two parallel chords such that AB = 24 cm.
Let the length of the CD be 2x cm.
Drop OE and OF perpendicular on AB and CD from the center O.
OE ⊥ AB and OF ⊥ CD
∴ OE bisects AB and OF bisects CD. ...(Perpendicular drawn from the center of a circle to a chord bisects it.)
⇒ AE = `24/2`
= 12 cm;
CF = `(2x)/2`
= x cm
In right ΔOAE,
OA2 = OE2 + AE2
⇒ OE2 = OA2 - AE2
= 152 - 122
= 81
∴ OE = 9 cm
∴ OF = EF - OE
= 21 - 9
= 12 cm
In right ΔOCF,
OC2 = OF2 + CF2
⇒ x2 = OC2 - OF2
= 152 - 122
= 81
∴ x = 9 cm
Hence, length of chord CD = 2x
= 2 × 9
= 18 cm.
APPEARS IN
संबंधित प्रश्न
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of
the circles. Show that:
(i) AB = CD,
(ii) AC = BD.

PQ and QR are two equal chords of a circle. A diameter of the circle is drawn through Q . Prove that the diameter bisects ∠ PQR.
A chord of length 8cm is drawn inside a circle of radius 6cm. Find the perpendicular distance of the chord from the centre of the circle.
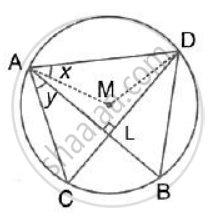
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y , Prove that : x = y
A chord of length 6 cm is drawn in a circle of radius 5 cm.
Calculate its distance from the center of the circle.
The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
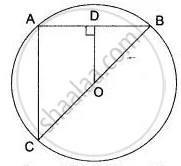
AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
AB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠ BAD and ∠ ACD.
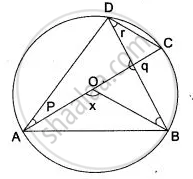
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.